円の接線 垂直 なぜ 230774-��の接線 垂直 なぜ
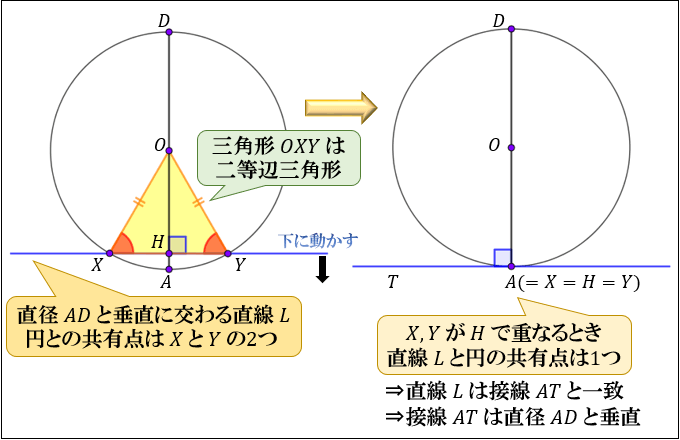
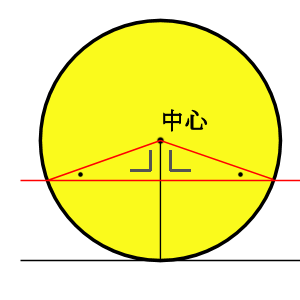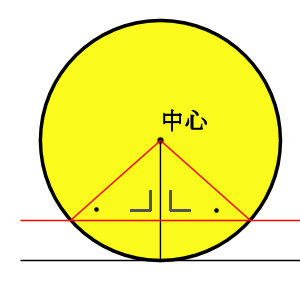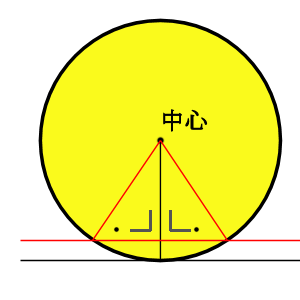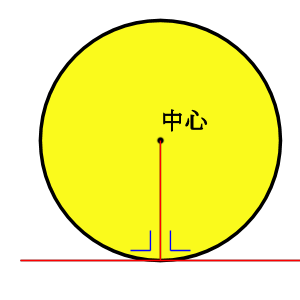
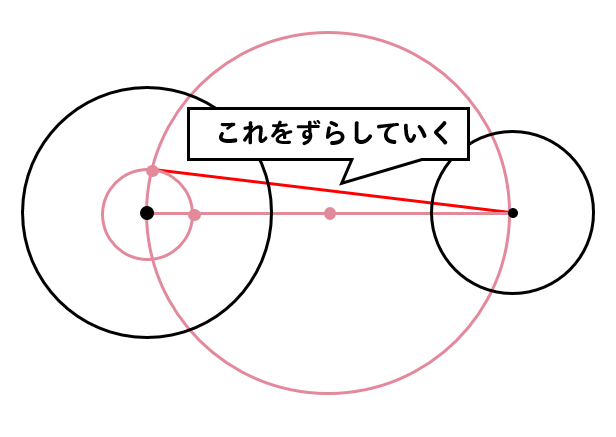
8/8/17 また、接線の傾きは、円の中心と接線を結んだ線と接線とが垂直に交わることから求めることができます。 接点が x 軸・ y 軸上にない場合、円の中心と接点を結んだ線の傾きは $\dfrac{y_1}{x_1}$ なので、接線の傾きは\ \frac{x_1}{y_1} \となります(参考: 基本垂直な直線9/8/18 円の接線が接点を通る直径と垂直になる理由 「円の接線 A T と、接点 A を通る直径 A D が垂直に交わる ∠ T A D = 90 ° 」ことは、直径 A D と 垂直に交わる直線 L を少しずつ下にずらしていくことで分かります。 直線 L と円の共有点を X, Y 、直径 A D と直線 L の交点を H としたら 三角形 O X Y は二等辺三角形になります。 そのため、直線 L を下にずらしていくと、 X と Y はどんどん H に17/2/19 こんにちは。 da Vinch (@mathsouko_vinch)です。 円の方程式は当たり前の式?直線をしっかりと考えた後はやはり円を式で書けるようになりたいところです。図形と方程式の元々のモチベーションは座標を用いて図形を表すことで

応用 90度に関連する作図 なかけんの数学ノート
円の接線 垂直 なぜ
円の接線 垂直 なぜ-ダウンロード No category;18/3/19 円の接線 高校受験などでよく出てきますね、 そこで円の接線の基本から作図、応用的な作図まで紹介します! 接線とは 接線の性質 円の外部の点を通る接線の作図 円の外部の点を通り円に外接する円の作図 (応用編)二つの円の共通接線の作図 (応用編)円の外部の二点を通り円に外接する円の




円の接線の方程式 おいしい数学
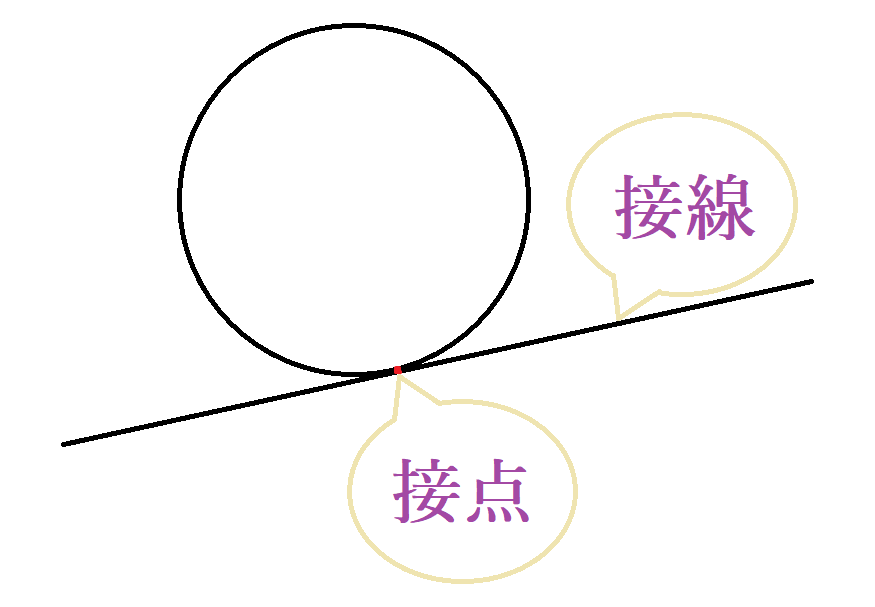
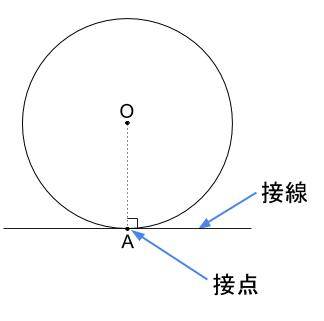
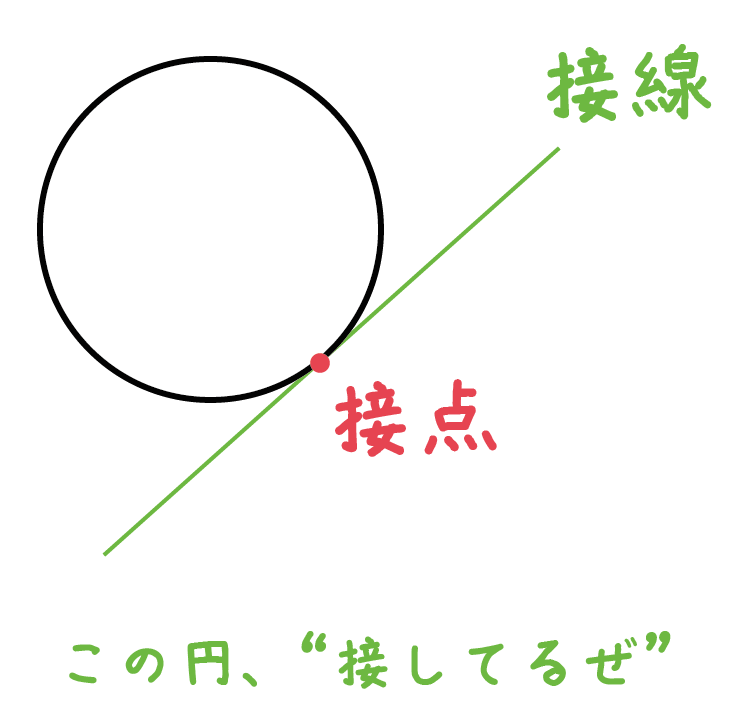
丸い折り紙-なぜ- 折り紙の円周が点 A と重なるように折り返すとき,円周上の点で点 A と 重なる点を Q とすれば,折り目をつけるということは, 点 A と円周上の点 Q の垂直二等分線を引くことになります. ところで,楕円には, 楕円上の任意の点を P9/8/19 スナップメニューは1回だけ有効なので、このとき接点が認識されるようになっていないのが原因でした。 終点も接線にする 終点も接線にしたいので再度スナップメニューで接線を選択しました。 カーソルを円に近づけると接線が認識されました。31/7/19 円の接線とは、円と1点だけを共有する直線のことです。 このときに共有する点(上の図では点 p )のことを接点といいます。 また、円の中心と接点を結んだ線分(半径)は、接線と垂直になります。これが円の接線が持つ重要な性質です。
25/2/21 1 接線とは・円の接点とは 2 円と接線の角度が90度であることの証明①:直線を平行移動 3 円の接線の角度が直角であることの証明②:角度が90度以外だと仮定して背理法で証明 4 円の接線が90度になることの証明③:辺の長さと角の大きさの大小関係の利用 5 接弦定理を使った円と接線の定理の証明は、卵が先か鶏が先かの問題に 6 まとめ10/3/16 2 円の接線の方程式・公式の証明 少し、複雑ですが、数学的に大事な平行移動の考え方が含まれているので、是非最後まで目を通して理解しましょう。 円1:(xa) 2 (yb) 2 =r 2 上の点n(x0,y0)の接線が (x0a)(xa)(y0b)(yb)=r 2 になる事を証明します。 方針2/7/ このように 「円の中心と接点を結んだ線分」 と 「接線」 は 必ず垂直 になります。これは幾何学の範囲で学んだことです。 ということは、このように考えるのはいかがでしょうか。 接線の方程式は、円の中心と接点を通る直線と垂直に交わる と。
10/9/19 円の接線は、中心と接点を結んだ線と垂直に交わる という知識を知っていないといけません。 これまたよく出題されるので覚えておきましょう。 垂線の作図まとめ! 最後に垂線の作図についてまとめておきましょう。/6/ こんにちは。 da Vinch (@mathsouko_vinch)です。この記事のトピックは「直線同士の関係である平行と垂直の条件を考える」です。 2つの直線の関係を式から考えるここでは直線同士の関係を式で表すことを考えます。なぜそんな それを少しずつずらして円の接点に向けていきます。 弦が短くなり交点の距離がだんだん短くなっていく感覚は 分かると思います。そして接点で一つになり、垂直なまま ずらしているので90°というわけです。
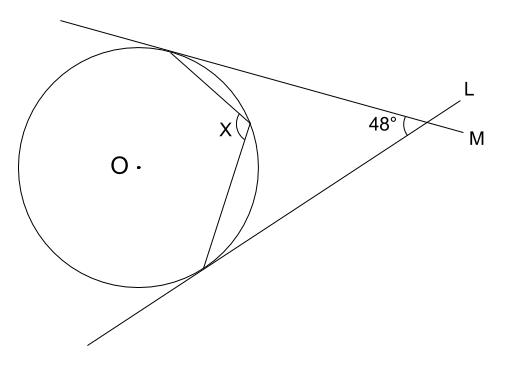



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ
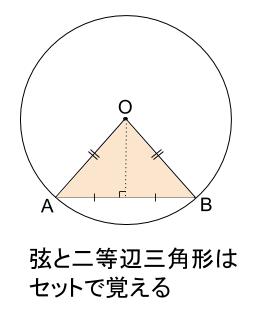
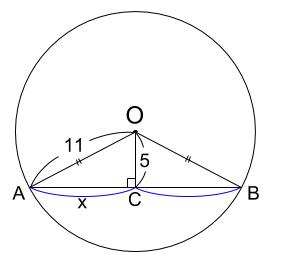
接線と半径は垂直 半径(正しくは円の中心と接点を結んだ線分)と、その点における接線は垂直 例題1 半径が \(11cm\) の円 \(O\) で、中心との距離が \(5cm\) である弦 \(AB\) の長さを求めなさい。 解答 このように、図が与えられないで出題されることもありポイント 円の接線の方程式の証明方法 Ⅰ 傾きを求める方法 Ⅱ 接点を通る直線を設定し,円と連立して接点で重解になることから導く方法 Ⅲ 点と直線の距離を使う方法 Ⅳ 法線ベクトルを使う方法 Ⅴ (数学Ⅲの)微分を使う方法 こうしてみると手段がなかなか円の接線の作図を思いつかないであろう。 導入では「ユークリッド原論に掲載されている作 図法」を紹介する。数学の歴史を振り返りながら, 作図の方法と,なぜその作図でよいのかを理解し, 「数学の歴史の奥深さ」を実感できる授業としたい。




なぜ垂直だとこの式になるのか分かりません Clearnote




円の接線の方程式 おいしい数学
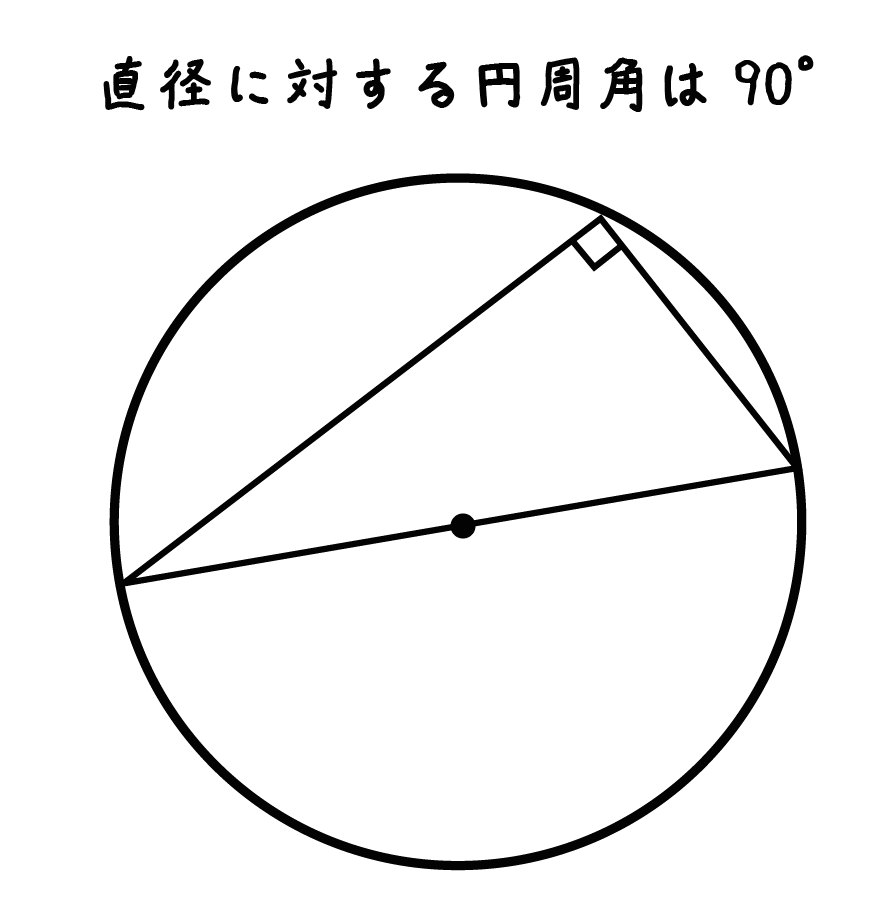
円の接線は接点を通る半径に垂直である。 証明 円Oの直径ABをとる。 点Bを通る接線と、点Aと円周上の点Cを結んで延長した線の交点をDとする。 ABDと BCDにおいて、 円の接線とその接点を通る弦の作る角は、その角の内部にある孤に対する円周角に等しいので、 ∠BAD=∠CBD 共通な角なので ∠ADB=∠BDC22/1/12 長くなるから図を書きながら考えてね (^_) 1 まず円O上に任意の点Aをとり、Aを通る円の接線をXYとする。 (接線上で点Xと点Yの間にAがあるイメージね) 2 円の接線が半径に対して垂直でないと仮定すると、角OAXまたは角OAYのどちらかは90度未満である。 (以下、角OAXが90度未満とします) 3 OからXYへ垂線をおろし、その足をHとする。 2の仮定より明らかにAとHは異なる22/5/ 直線に垂直な円の接線の方程式を求める 直線 $axbyc=0$ に垂直な、中心が $ (x_0,y_0)$ 半径が $r$ の円 $ (xx_0)^2 (yy_0)^2=r^2$ の2つの接線の方程式を求める。 求める接線は、直線 $axbyc=0$ に垂直なのでその方向ベクトルは、直線の法線ベクトルになる。 直線 $axbyc=0$ の法線ベクトルは、 $$\vec {n}= (a,b)$$ よって接線の傾き $m$ は、 $$m=\frac




三角形の外心が3辺の垂直二等分線の交点で求められるのはナゼ 数学について考えてみる




垂線の作図 手順と なぜ について解説します 中学数学 理科の学習まとめサイト
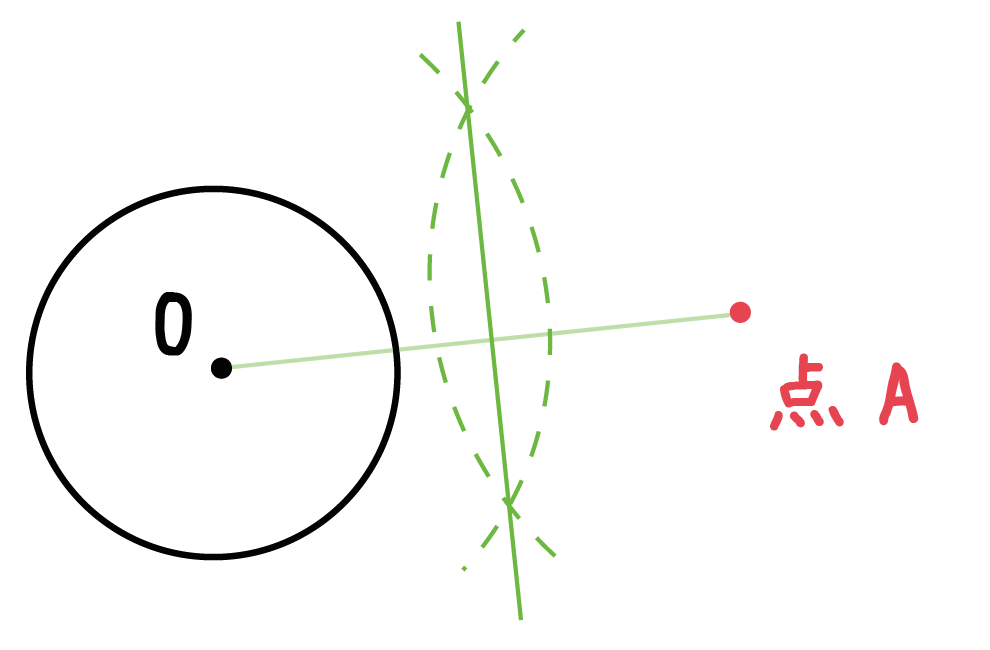
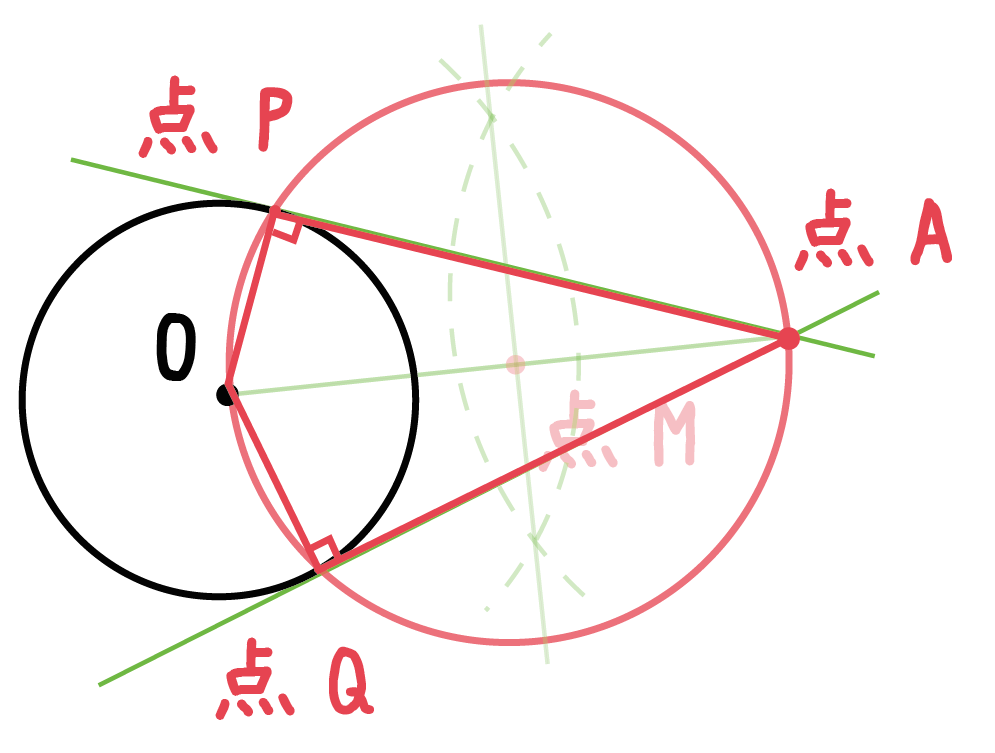
25/4/19 円運動の速度 それでは円運動の速度を考えます。 まず円運動では半径が一定ですから、 中心方向の速度は0 です。 次に接線方向の速度です。 以下の図を見てください。 時間\(\Delta t\)の間に中心角が\(\Delta\theta\)進んだ場合、中学生の数学でよく使うアルファベット文字の意味 「角すいの体積は " 底面積×高さ×1/3 "」になる説明19/3/15 さっきの「円の接線の性質」、 円の接線は、その接点を通る半径に垂直である をつかえば、 線分pa、qaは円の接線 ってことになるんだね。 これは中2数学でならう内容だから、今はまだわからなくても大丈夫だよー。 まとめ:円の接線の作図は2パターンしかない
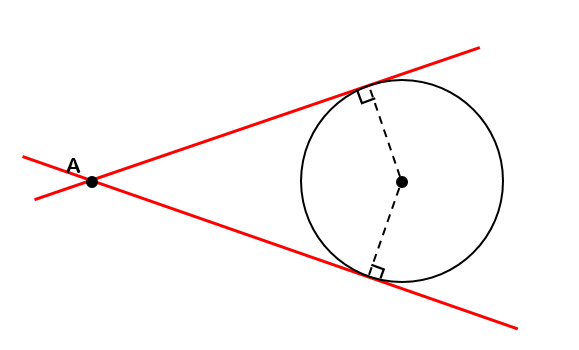



円の接線作図 基本作図から2つの円の共通接線まで解説 数スタ




どうしてこの手順で求まるのでしょうか 教えていただきたいです Clearnote
一つ問題なのが、接弦定理を証明するのに、円の接線が半径に対して垂直になることを用いるような気がします。 背理法を使うこんな証明を見たことがあります。 1 円O上に任意の点Aをとり、Aを通る円の接線をXYとする。 (接線上で点Xと点Yの間にAがあるイメージです) 2 円の接線が半径に対して垂直でないと仮定すると、角OAXまたは角OAYのどちらかは90度未満である。 (以2/9/06 中1です 円の接線に垂直で接点を通る線が、必ず円の中心を通る理由を教えてください 数学 カヴァリエリの原理について カヴァリエリの原理は、高校までの範囲では きちんと証明が出来ないから、定理ではなく 原理と言われています。ここでは、なぜ「円の接線は、接点を通る半径に垂直」なのか? を、考えていきます。 この公式のポイント ・円の接線は、その接点を通る半径に垂直に




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学




平面図形 円の接線はなぜ接点を通る半径に垂直なのか Youtube
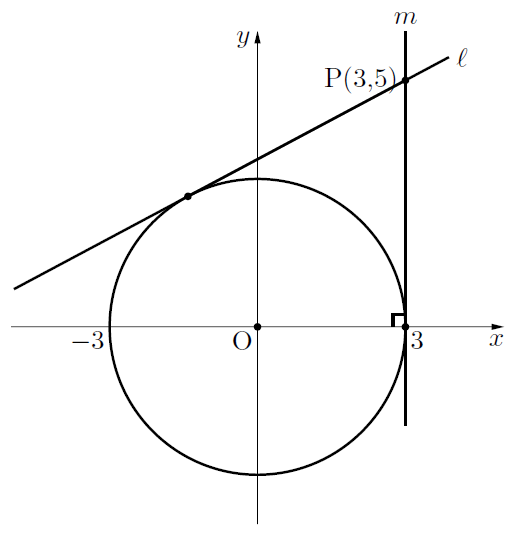
25/2/05 「円の接線は、接点を通る半径に垂直である。 」 これを方冪(ほうべき)の定理(円の接線の性質)と言います。 中学生の段階では、他の定理と同じ様に、 「こういう事が成り立つんだ」と理解していれば良いと思います。 証明しようとすると、 接線がx軸に垂直ならば接線がx=3の直線にならなければいけませんよね? また垂直な接線なら接点は円の右端か左端になります。 円の情報(中心と半径)から、それはありえないのでx軸と垂直ではないとわかります。 記述が必要かはよくわからないので先生に聞いた方がいいかと思いますが接点 :円と接線の交わる点のこと 2つの直線が(互いに) 垂直 である: それら2つの直線の一方を適当に平行移動させた時、直角をなすこと 公理(証明なしに正しいとみなす主張) 三角形の2つの辺をとる。 それらの辺の大小関係は、それぞれの対角の大小関係に一致する。 ユークリッド平面上では、平行でない直線はただ1点で交わる。 証明したいこと 円の接線は、接点を通る半径に垂直である
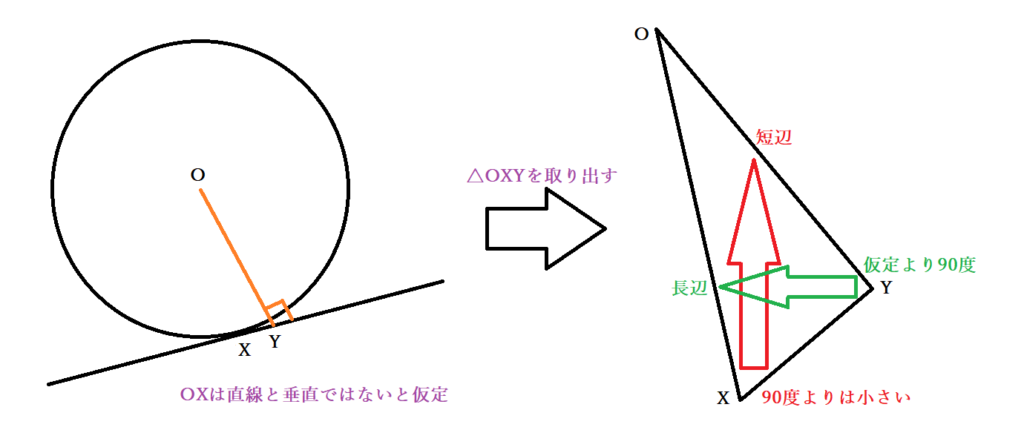



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの学びblog
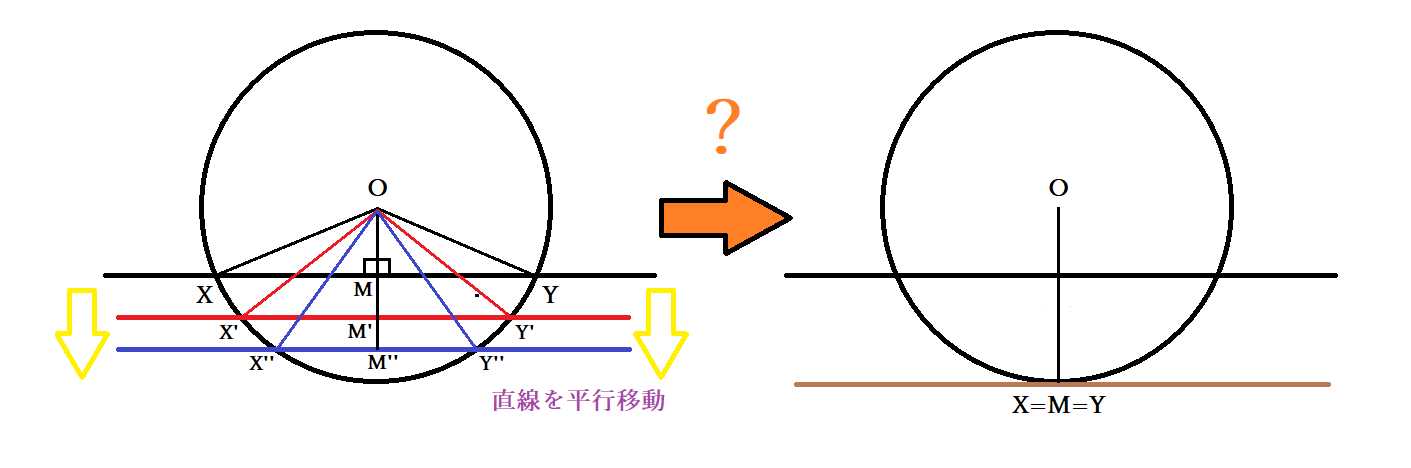



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの学びblog



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



弦の垂直二等分線は円の中心を通るのはなぜですか 教えてください Yahoo 知恵袋



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく
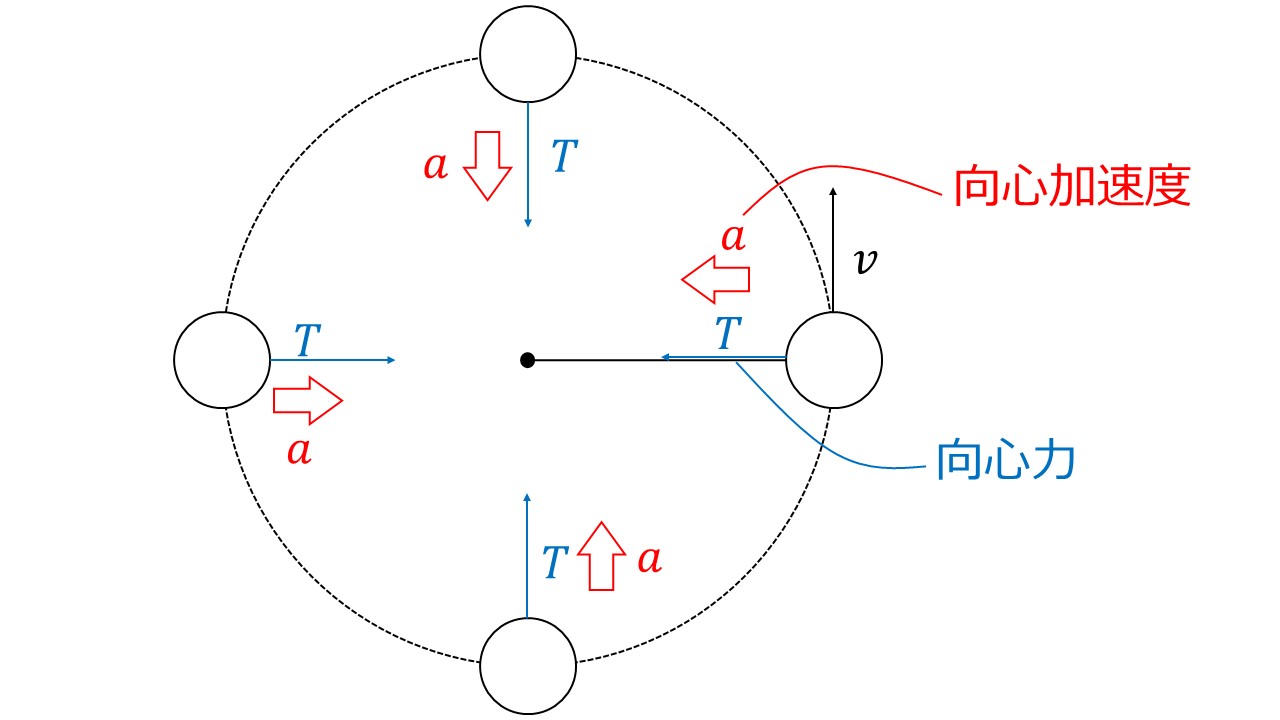



等速円運動の2つの解法 向心力と遠心力についても解説しています 大学受験の王道




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学
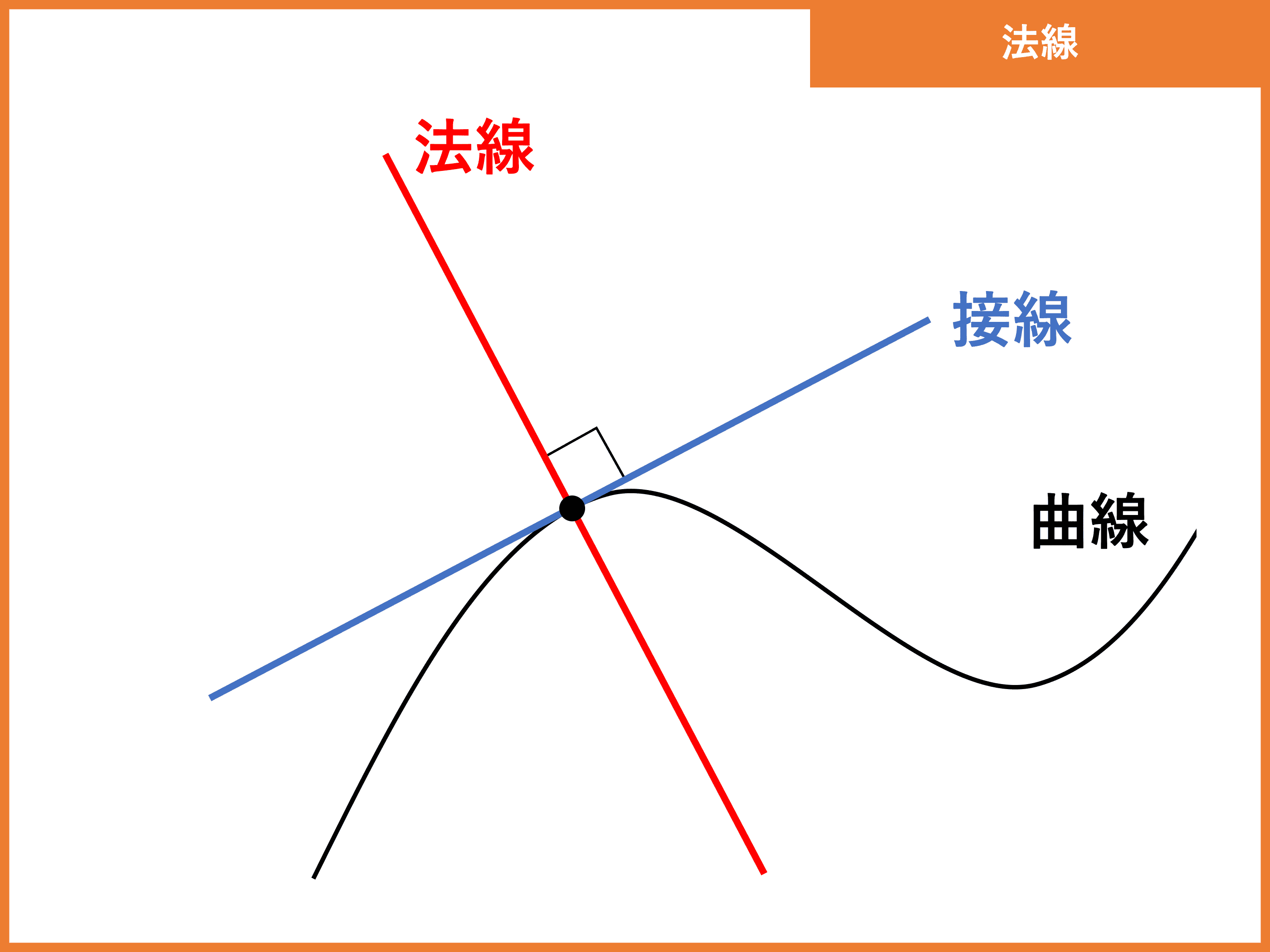



法線とは 法線の方程式や法線ベクトルの公式 求め方 受験辞典
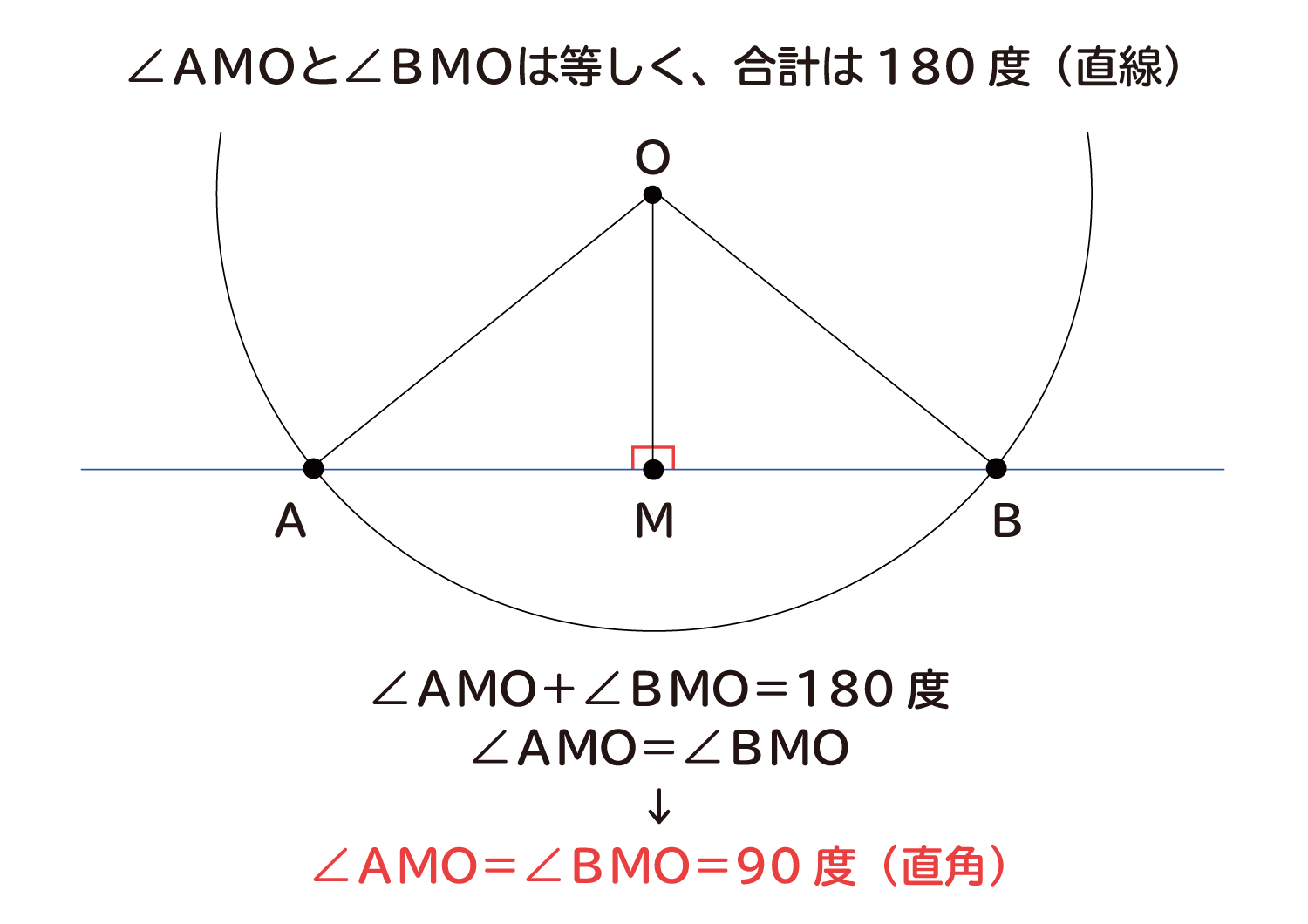



なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル



円の接線は 接点を通る半径に垂直なのはなぜですか 教えてください よろし Yahoo 知恵袋
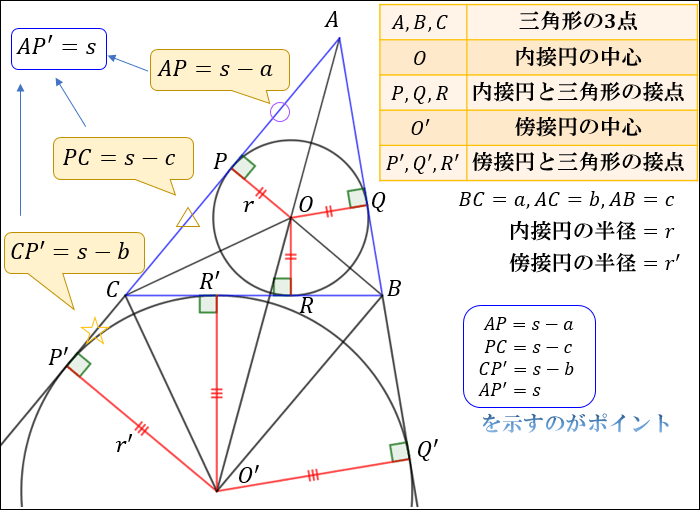



ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ



円の接線は 接点を通る半径に垂直なのはなぜですか 教えてください よろし Yahoo 知恵袋




応用 90度に関連する作図 なかけんの数学ノート
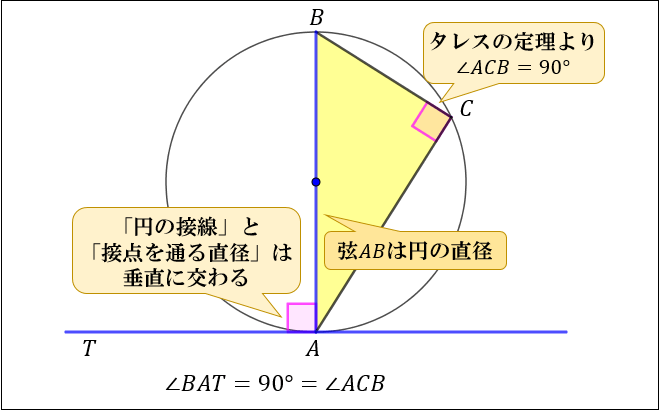



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ




2 の問題でなぜマイナスがつき 分子分母が逆になるのか分かりません Clearnote




円の接線の方程式 おいしい数学




垂線の作図 手順と なぜ について解説します 中学数学 理科の学習まとめサイト
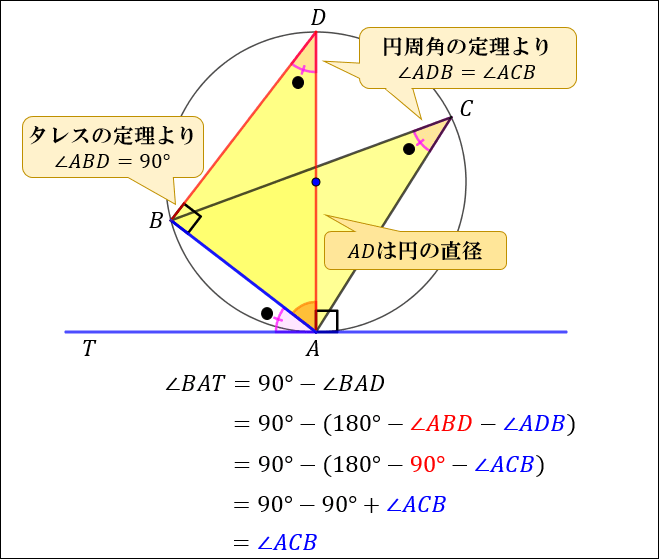



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ
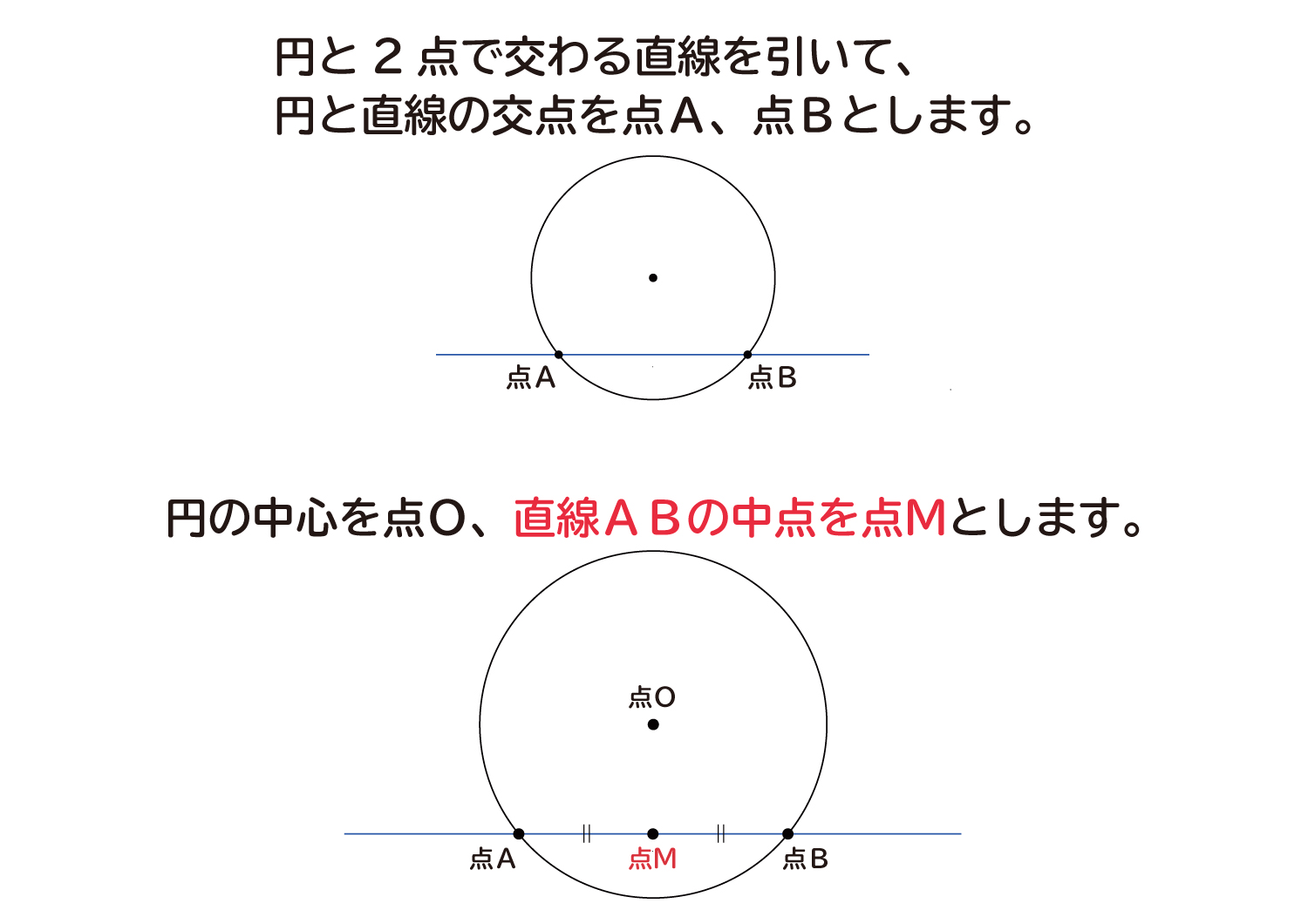



なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル
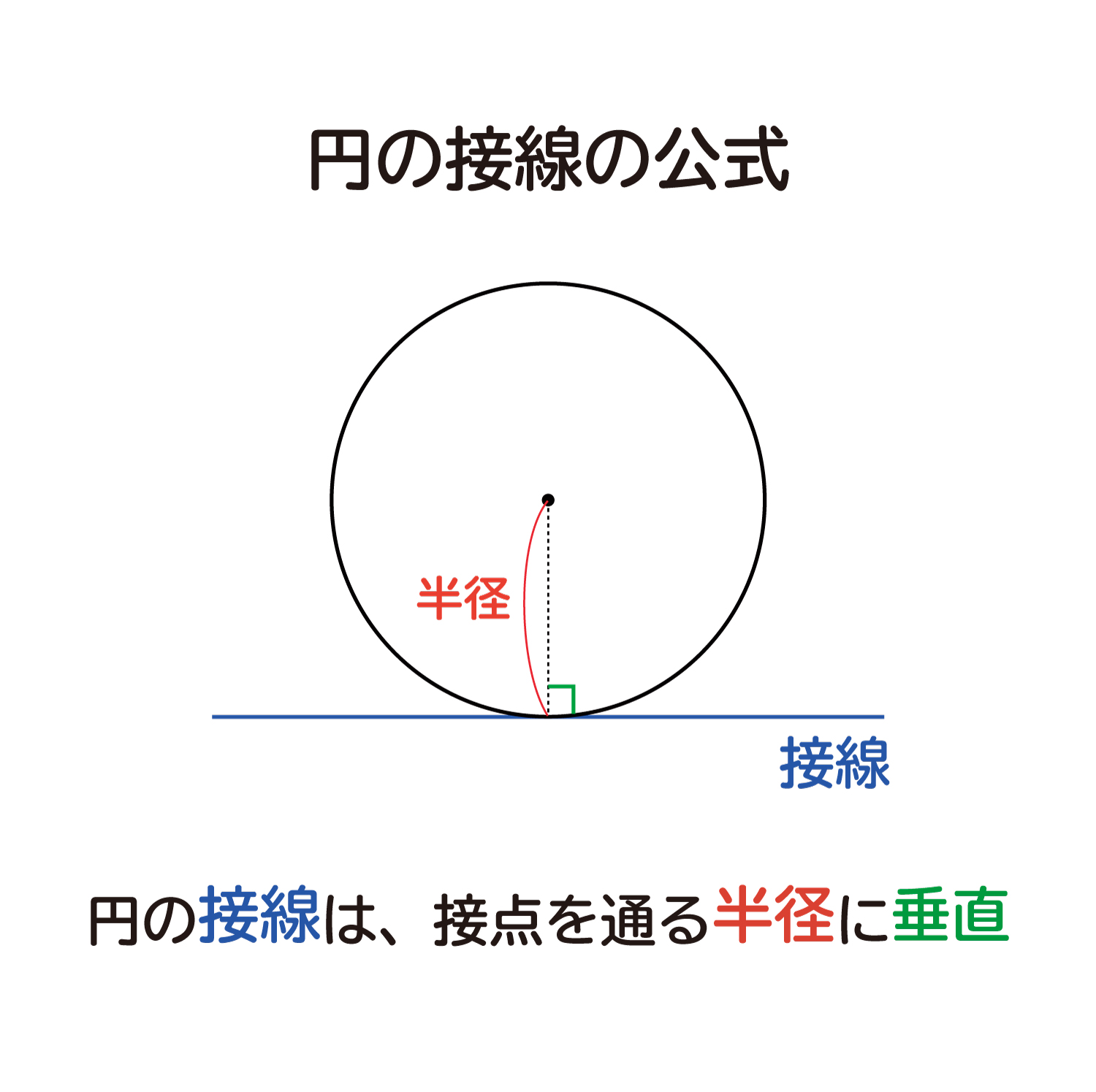



なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル




円の接線の方程式を求める公式と証明 高校数学の知識庫




第3巻命題18 接線と半径は垂直 Stoixeia ストイケイア




双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ



証明 円の接線は接点を通る半径に垂直である




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ
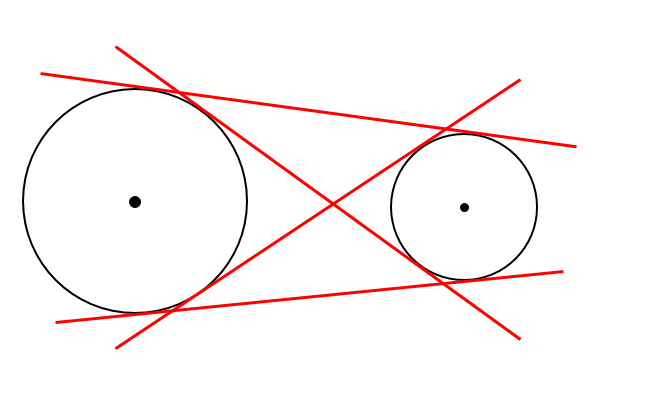



円の接線作図 基本作図から2つの円の共通接線まで解説 数スタ
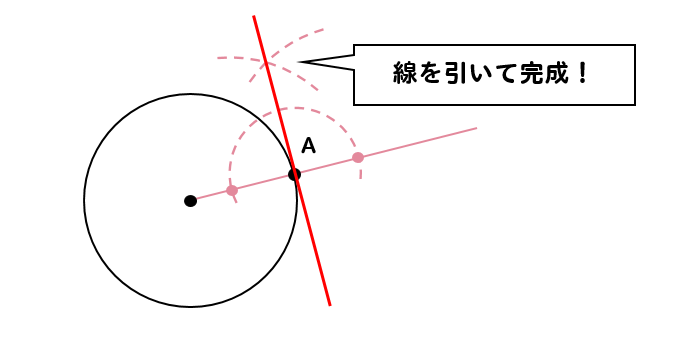



円の接線作図 基本作図から2つの円の共通接線まで解説 数スタ



中学数学 三平方の定理 円と接線 弦 中学数学の無料オンライン学習サイトchu Su




三角形の内心が角の二等分線の交点で求められるのはナゼ 数学について考えてみる



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの学びblog



1



円と接線




円の接線の方程式を求める公式と証明 高校数学の知識庫
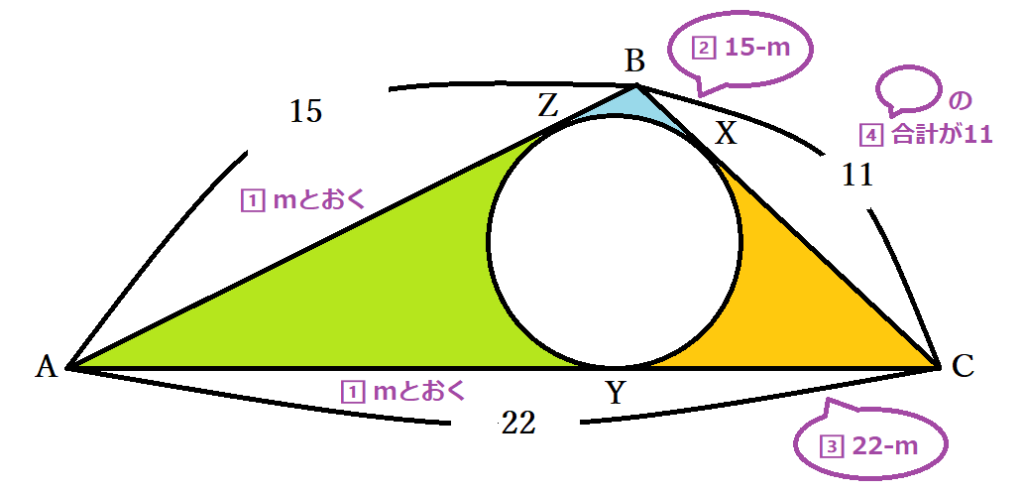



円の接線の性質 公式 円外の点pを通る円oの接線の長さが等しいことの証明 中学数学 Curlpingの学びblog



1
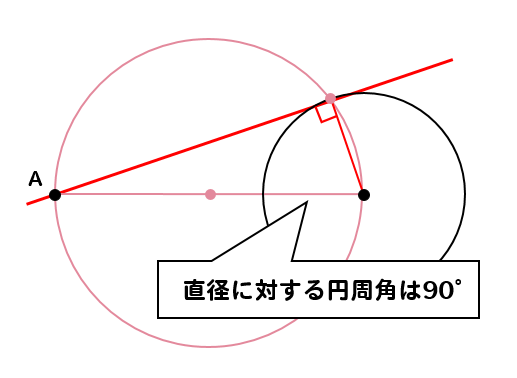



円の接線作図 基本作図から2つの円の共通接線まで解説 数スタ




垂線の作図 手順と なぜ について解説します 中学数学 理科の学習まとめサイト




基本 垂線の作図 直線上にない点を通る その2 なかけんの数学ノート




垂線の作図 手順と なぜ について解説します 中学数学 理科の学習まとめサイト
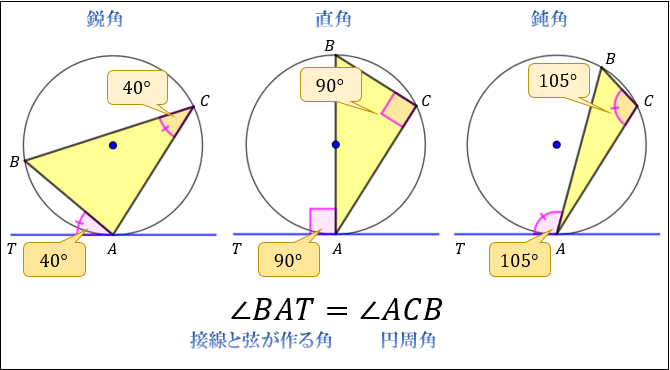



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



至急 高一数学の問題 次の円の接線の方程式と そのときの接点の座標を求めよ Yahoo 知恵袋
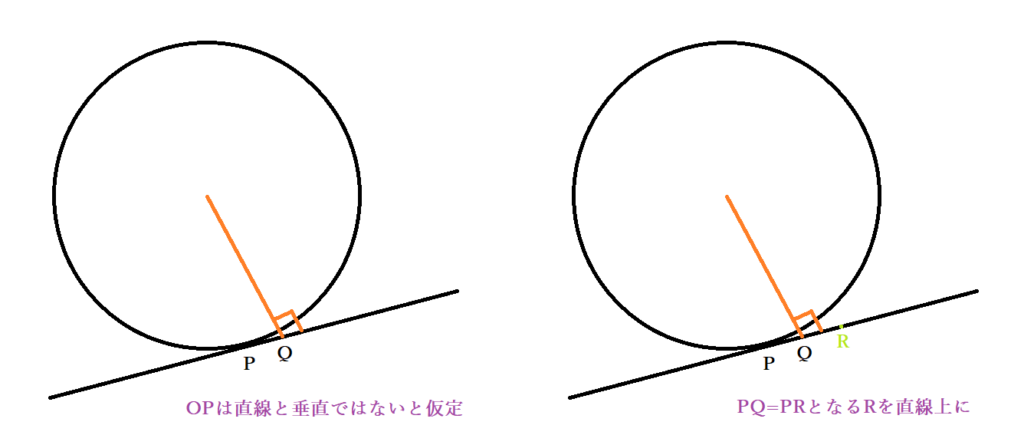



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの学びblog




この問題の2番の問題のマーカー部分がなぜそう言えるのかが分からないです 解説 Clearnote
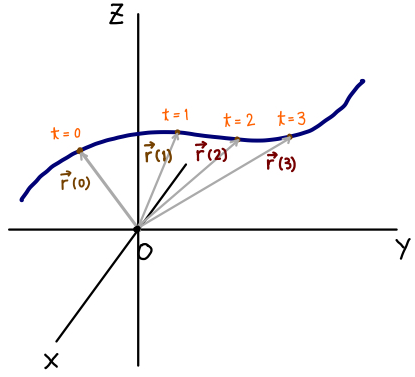



F の勾配が等位面に垂直であるのはなぜか ベクトル解析 基礎からの数学入門
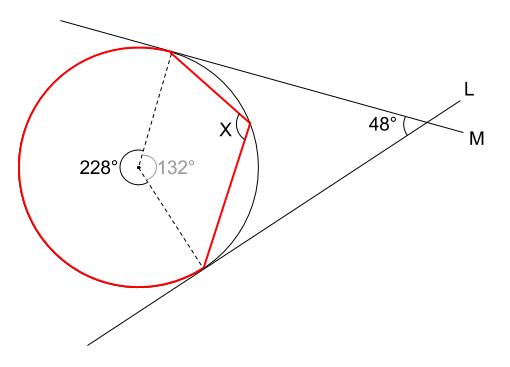



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su




物理のエッセンス力学編番 Koko物理




円の接線の方程式を求める公式と証明 高校数学の知識庫



中学数学 三平方の定理 円と接線 弦 中学数学の無料オンライン学習サイトchu Su



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく




まず どうしたらx軸に垂直でないことがわかるのでしょうか できればなぜ垂 Clearnote



数学a 平面図形 円の性質 円の接線



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく




Amazon Com Mathematics Formula For Difficult High School Passes Do You Answer In 10 Seconds Math Formula Japanese Edition Ebook Yoruhayonetaro Kindle Store



中学数学 三平方の定理 円と接線 弦 中学数学の無料オンライン学習サイトchu Su
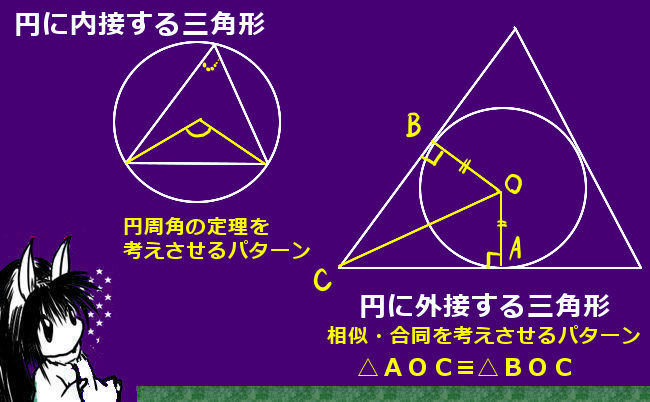



円の接線と内接 外接 理数系学習サイト Kori




なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル




ベクトル方程式 5 怜悧玲瓏 高校数学を天空から俯瞰する
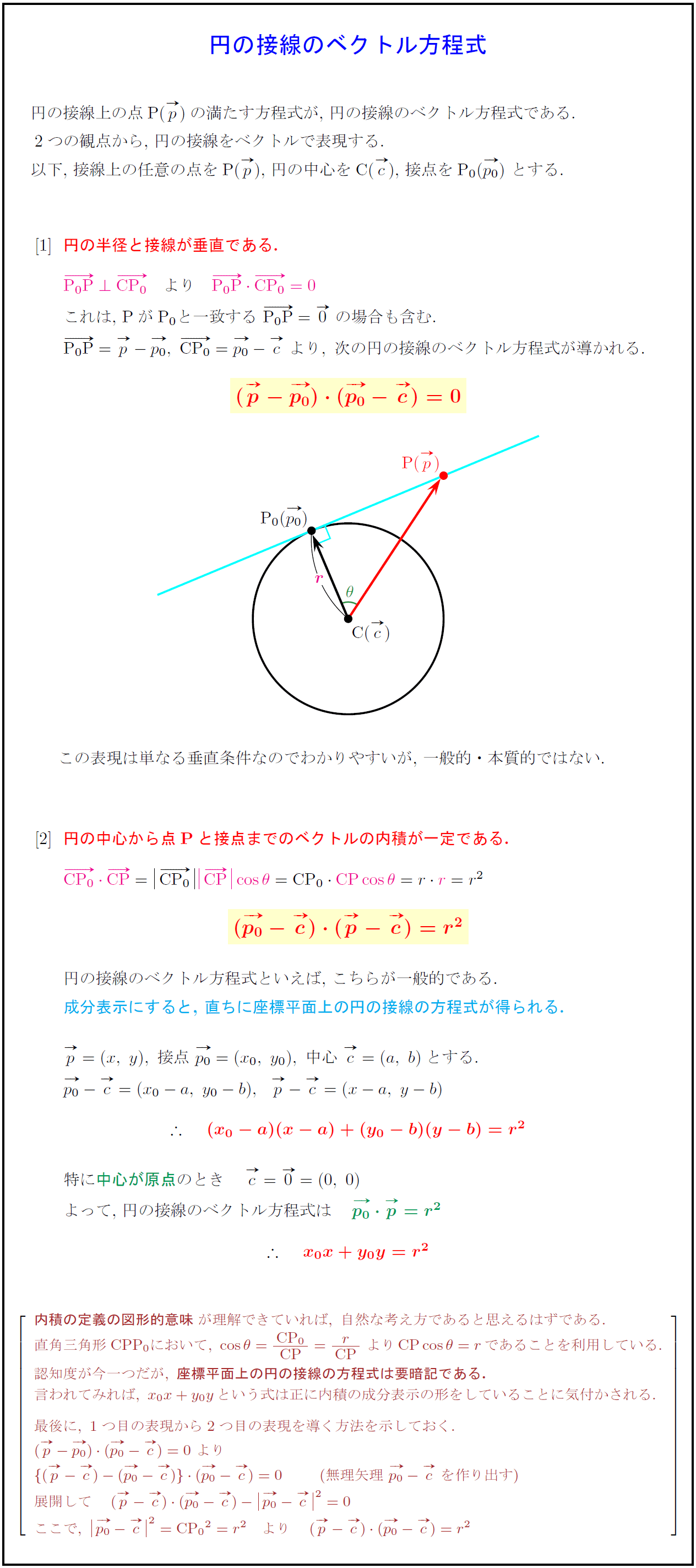



高校数学b 円の接線のベクトル方程式2パターン 受験の月



2つの円x 2 Y 2 1と X A 2 Y 2 A 2 4 Yahoo 知恵袋



中学数学について質問します 何故円の接線に垂直な線は円の中心を通るのです Yahoo 知恵袋




Euclidea 2 9 Web版2 8 点で円に接する接線の作図 解説 みのまわりのものたち




Amazon Com Mathematics Formula For Difficult High School Passes Do You Answer In 10 Seconds Math Formula Japanese Edition Ebook Yoruhayonetaro Kindle Store




丸い折り紙4




円の接線の方程式を求める公式と証明 高校数学の知識庫
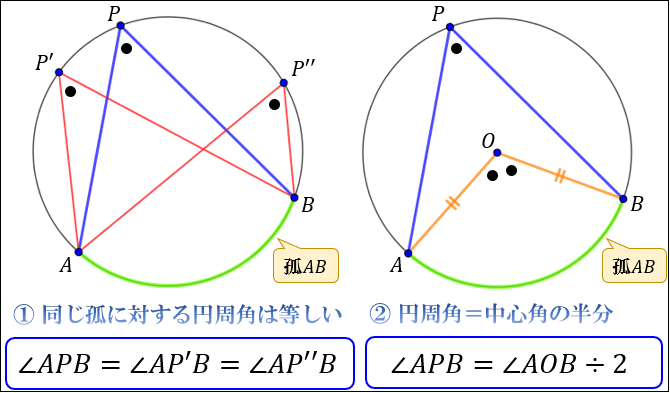



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ




68 数b ベクトルと円の接線の方程式 Youtube




応用 2つの円の交点を通る円や直線 なかけんの数学ノート




応用 90度に関連する作図 なかけんの数学ノート
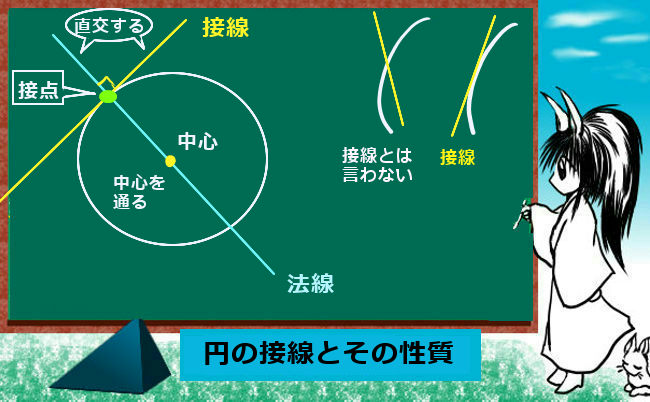



円の接線と内接 外接 理数系学習サイト Kori



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく



円の接線作図 基本作図から2つの円の共通接線まで解説 数スタ




三角形の内心が角の二等分線の交点で求められるのはナゼ 数学について考えてみる



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su




円の接線の長さの証明 数学a By となりがトトロ マナペディア



Emath 高校数学 円の接線 円の外部から2 数樂管理人のブログ




第3巻命題18 接線と半径は垂直 Stoixeia ストイケイア



何故 この方法で円の接線の作図ができるか分かりません 教えて Yahoo 知恵袋
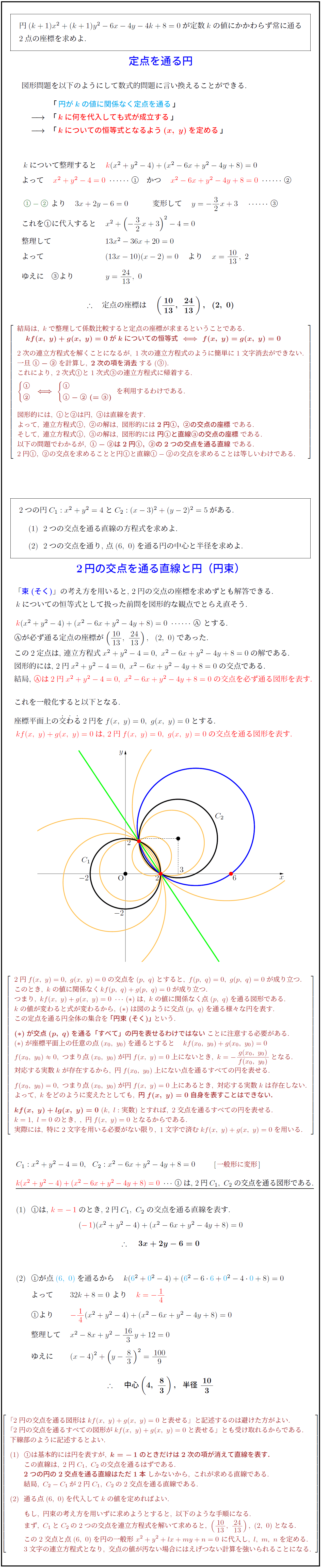



高校数学 定点を通る円 2円の交点を通る直線と円 円束 受験の月




円の接線が半径に垂直であることの証明 Youtube
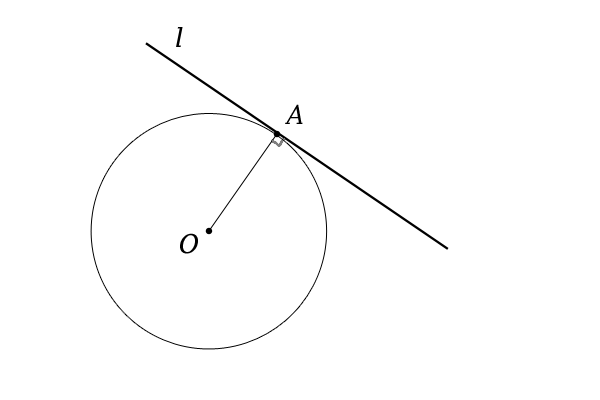



円と直線の距離と位置関係 特に交点 接点 接線について 高校数学マスター
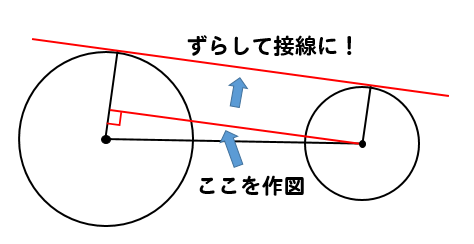



円の接線作図 基本作図から2つの円の共通接線まで解説 数スタ
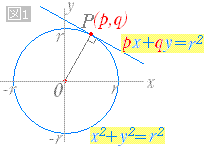



円の接線の方程式




なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル




線を引いたところが分かりません どこから導いたのですか 解説お願いします Clearnote
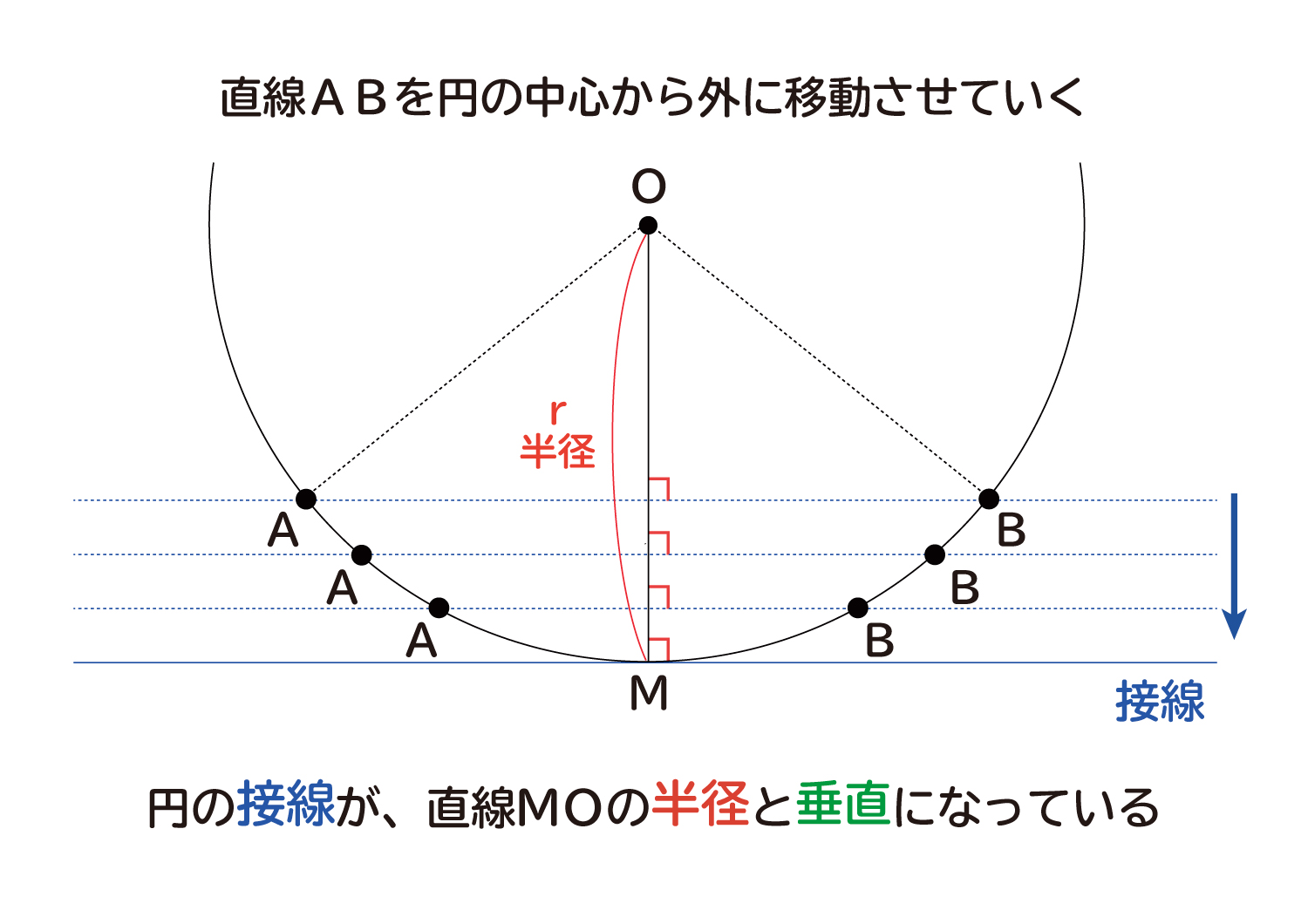



なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル
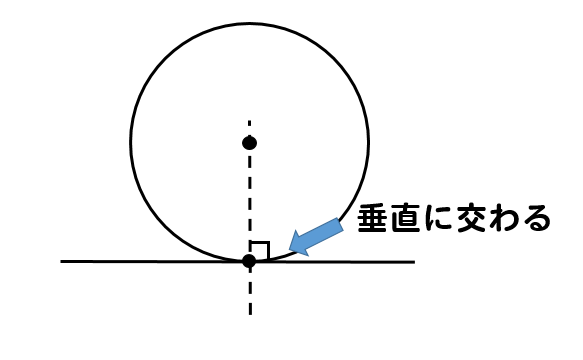



円の接線作図 基本作図から2つの円の共通接線まで解説 数スタ




三角形の内心が角の二等分線の交点で求められるのはナゼ 数学について考えてみる
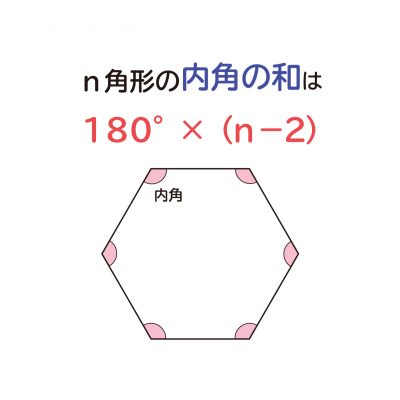



なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル



1



1




証明 円の接線は接点を通る半径に垂直である
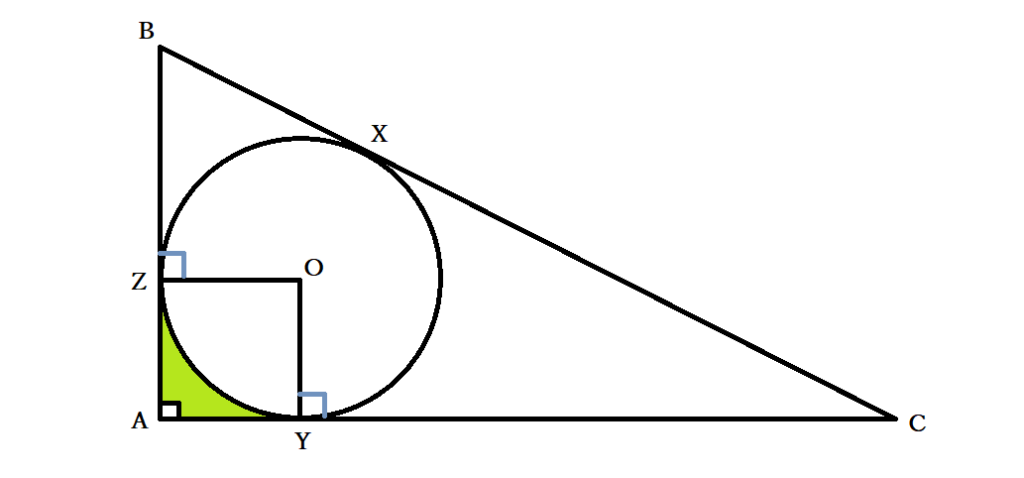



円の接線の性質 公式 円外の点pを通る円oの接線の長さが等しいことの証明 中学数学 Curlpingの学びblog




円の接線の方程式 おいしい数学
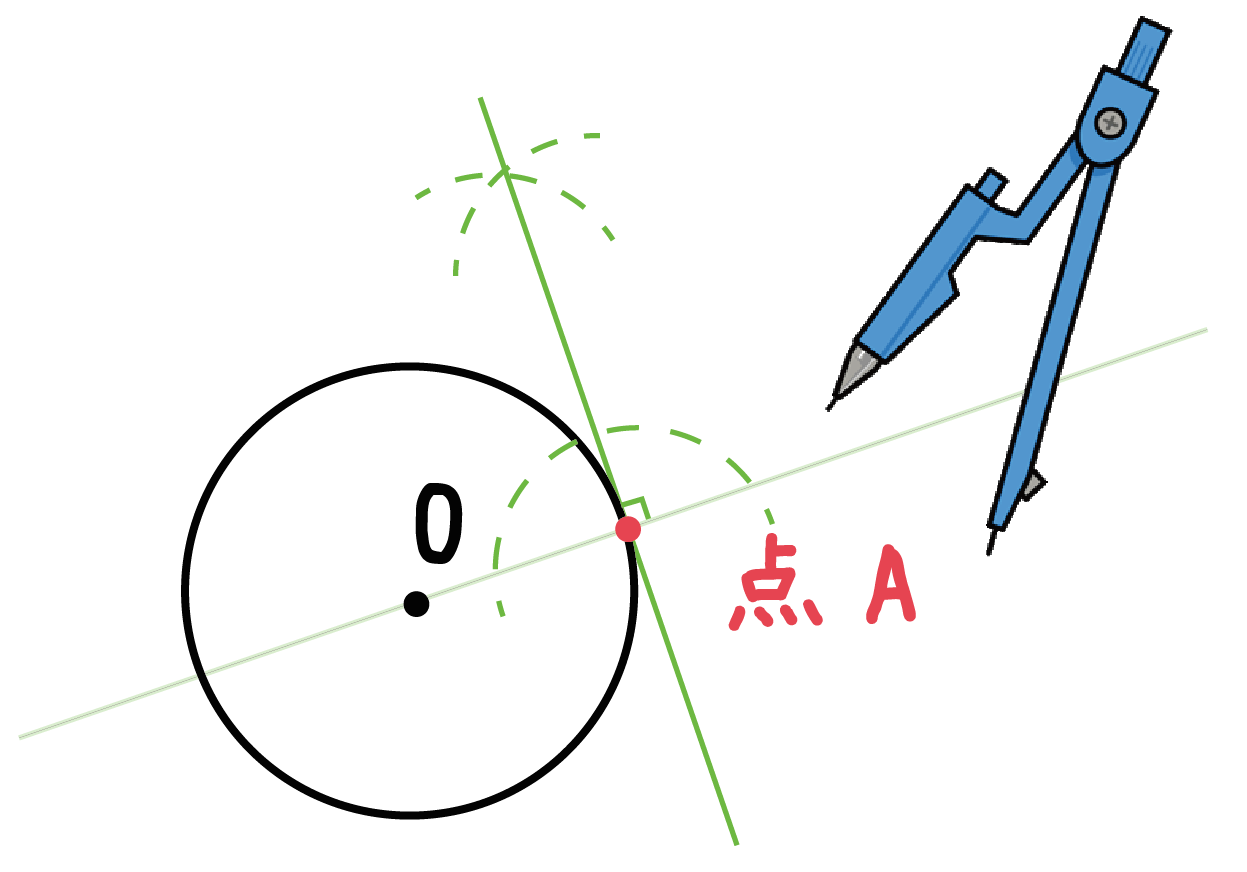



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく
コメント
コメントを投稿